一篇论文

摘要

目标跟踪是计算机视觉领域的重要研究课题，它在视频监控、无人驾驶、人机交互中均有着广泛的应用。虽然目标跟踪算法近年来得到了长足的发展，但是由于目标形变、遮挡、快速运动以及低光照度等不利因素，这使得目标跟踪依然面临着巨大的挑战。

本文以DSST算法作为基础，设计了一种基于自适应模板更新的目标跟踪算法。具体来说，我们使用了峰值旁瓣比来评估跟踪结果的可靠性，只有在跟踪结果可靠时才进行模板更新，进而改进了算法中固定的每帧都更新的弊端。峰值旁瓣比PSR的作用主要是用于测量峰值强度，通过检测每一帧图像的PSR峰值强度，我们可以得到关于响应图中响应值的聚集程度信息。PSR的值越大，响应值的聚集程度越高，那么跟踪结果越准确。由已有的研究工作得知，一般情况下当PSR的值高于7时跟踪效果是比较良好的，而在低于7之后则意味着跟踪器出现了漂移甚至是丢失了目标，因此，PSR可以作为评估目标模板是否被污染的依据。在TColor-128数据集上的实验表明，改进后的算法较于原DSST算法在精确度和成功率这两方面上有了大幅提升。此外，与其他先进算法相比，我们的算法也取得了具有竞争力的性能。

关键词： 目标追踪，自适应更新，相关滤波，峰值旁瓣比（PSR）

---

ABSTRACT

Object tracking is an important research topic in the field of computer vision, and it has a wide range of applications in video surveillance, unmanned driving, and human-computer interaction. Although target tracking algorithms have made great progress in recent years, target tracking still faces huge challenges due to unfavorable factors such as target deformation, occlusion, fast motion, and low light illumination.

Based on DSST algorithm, this paper designs a target tracking algorithm based on adaptive template update. Specifically, we use the peak sidelobe ratio to evaluate the reliability of the tracking results, and only update the template when the tracking results are reliable, thereby improving the fixed update every frame in the algorithm. The role of the peak sidelobe ratio PSR is mainly used to measure the peak intensity. By detecting the PSR peak intensity of each frame image, we can obtain information about the aggregation degree of the response values in the response map. The larger the value of PSR, the higher the aggregation degree of the response values, and the more accurate the tracking result. According to the existing research work, in general, when the PSR value is higher than 7, the tracking effect is relatively good, and when the value is lower than 7, it means that the tracker drifts or even loses the target. Therefore, the PSR value is It can be used as a basis for evaluating whether the target template is contaminated. Experiments on the TColor-128 dataset show that the improved algorithm has a significant improvement in accuracy and success rate compared to the original DSST algorithm. Furthermore, our algorithm also achieves competitive performance compared to other state-of-the-art algorithms.

Keywords: Target tracking, Adaptive update, Correlation filtering, PSR (Peak to Sidelobe Ratio)

---

第一章 绪论

研究背景与意义

目标跟踪是计算机视觉技术中的重要组成部分 ¹ ，对视频信息有很好的的分析与处理能力，再加上计算机硬件的日益革新，快速变化的现实世界和生活环境让这项技术有了越来越多的应用场景，例如人机交互²、智能监控³、智能交通⁴、军事领域⁵、医疗诊断⁶等。

此外，目标视觉跟踪技术在虚拟现实、无人机、汽车自动驾驶等方面也有广泛应用。随着科技的发展和人们物质生活的提高，目标跟踪技术在现实生活中扮演者越来越重要的角色，然而在研究这项技术过程中也伴随着诸多难题，如运动目标速度过快、尺度变化、复杂的背景以及遮挡等都会直接影响到跟踪的准确度和鲁棒性。因此，为了让目标跟踪技术更好地应用在生活中，我们有必要对目标跟踪技术做进一步的研究。

国内外研究现状

目标跟踪技术在计算机视觉领域是重要分支，拥有广泛的发展前景，目前在各类实际应用得到了良好实现，例如人和计算机之间的交互、智能监控系统、医疗系统等。以往的数年时间里，目标跟踪得到了稳定的发展，并且大量新的理论方法陆续被学者或科研人员所提出，获得了许多可喜的成果。从大体上来看，目标跟踪技术是在这几个方面加以完善，例如模型优化、特征表示、评估机制、搜索机制等。但是，由于这项技术在我们的日常生活中的应用越来越广，人们对它的性能有了更加严格的要求。下面我们将介绍几类算法。

基于检测的跟踪算法

由于分类器适合在线学习，因此基于检测的跟踪框架引起了广泛的关注，例如支持向量机（SVM, Support Vector Machines）⁷，随机森林分类器⁸或增强变体，并且可用于实时跟踪。对于每一帧，收集了一组正、负样本，以逐步学习判别分类器，以将目标与其背景区分开。但是，提取样品学习在线分类器可能会导致样本歧义问题，而在标签样品中的轻微错误可能会影响分类器性能并逐渐导致跟踪器漂移。为了减轻样本歧义引起的模型更新的问题，先前的研究已经做出了相当大的努力，例如多个实例学习（MIL, Multiple Instance Learning）⁹，半监督学习，和P-N学习¹⁰。此外，文献¹¹中提出了一个包含整体模板和局部表示的鲁棒外观模型，以处理急剧的外观变化。同样，使用1类SVM和结构化输出SVM的学习框架¹²被设计用于协作描述性组件和用于跟踪的判别性组件。此外，文献¹³中构建了多个具有不同学习率的分类器以解决模型漂移问题，而不是仅学习单个分类器。通过减轻样本歧义问题，上述方法在最近的基准数据集中取得了可观的的性能效果¹⁴。

基于相关滤波器的跟踪算法

基于相关滤波器跟踪器的两个重要优势分别是高计算效率和优异的精度。通过将模型转移到傅立叶域中，矩阵代数可以通过逐元素运算来求解。Bolme等人提出了最小输出平方和误差（MOSSE, Minimum Output Sum of Squared Error）方法¹⁵，并在灰度图像上学习了最小输出平方和误差滤波器，该滤波器使用强度特征来表示对象。Heriques等人提出了用核检测跟踪的循环结构（CSK, Circulant Structure of tracking by detection with Kernel）算法¹⁶，该算法通过利用训练样本的循环结构将过滤器转换到傅立叶域。在他们的工作中，CSK在基准数据集上具有相当大的性能，实现了最高的跟踪速度。作为对CSK的扩展，在核化相关滤波器（KCF, Kernelized Correlation Filter）中使用了定向梯度直方图（HOG, Histogram of Oriented Gradients）特征以及高斯核岭回归。判别尺度空间相关滤波跟踪器（DSST, Discriminative Scale Space Tracking）学习了具有比例金字塔表示的判别相关滤波器，来处理目标对象的尺度变化。他们学习了两种滤波器，一种用于平移估计，另一种用于尺度估计。此外，具有多特征跟踪器（SAMF, Scale Adaptive with Multiple Features tracker）的尺度自适应通过训练KCF在各种大小的图像块上，围绕最新估计位置搜索目标来估计尺度变化。Huang等人提出了畸变抑制相关滤波器¹⁷，通过引入正则化项以限制响应图，他们的方法能够抑制由背景噪声信息和跟踪对象的外观变化所引起的异常。

手工制作的特征已被广泛用于基于相关滤波器的跟踪中，并且最近已经开始将深度特征与相关过滤结合使用，以发挥其巨大潜力。为了遵循端到端的理念，Valmadre等人¹⁸将判别相关滤波器（DCF, Discriminant Correlation Filter）整合到siamese框架¹⁹中，作为一层卷积神经网络（CNN, Convolutional Neural Network）进行端到端训练。其他一些DCF方法重点在整合已训练好的深度学习网络里的卷积特征。 Ma等人提出了一种独立DCF跟踪器的分层集合方法²⁰，以组合多个卷积层。 Danelljan等人提出了连续卷积算子跟踪器（C-COT, Continuous Convolution Operator Tracker）²¹，以有效整合多分辨率的浅层和深层特征图。高效卷积算子（ECO, Efficient Convolution Operators）²²跟踪器从三个级别进一步优化了C-COT跟踪器的速度和准确性：型号尺寸，训练集大小和模型更新。由于CNN特征的高复杂性，具有深度特征的跟踪器的速度并不优于传统的手工特征跟踪器。

长期跟踪的方法

具有短期记忆的相关滤波器在处理对象遮挡和消失方面具有很大的局限性。因此，许多方法旨在让相关过滤器具有长期记忆来实现更高级的跟踪。短期跟踪器和检测器的组合是一种常用的长期跟踪器结构，最初用于跟踪学习检测（TLD, Tracking-Learning-Detection）²³。Kalal等人开创性地提出了一种无记忆的流群作为短期跟踪器和基于模板的检测器²⁴。Ma等人提出使用KCF作为短期跟踪器和随机蕨分类器作为检测器来构建长期跟踪器²⁵。同样，Hong等人将KCF跟踪器与基于尺度不变特征变换（SIFT, Scale-Invariant Feature Transform）的检测器组合在一起²⁶，该检测器也用于检测遮挡。Dai等人通过使用辅助重新检测来建立了一个简化的长期跟踪器²⁷，该追踪器将短期组件与SVM分类器结合在一起，以构建长期组件。Alan等人利用新型DCF约束滤波器学习方法设计了能够有效地重新检测到整个图像中的目标检测器²⁸。并且，他们建议使用相关响应值和峰值旁瓣比（PSR,Peak to Sidelobe Ratio）²⁹来评估跟踪失败。Sun等人将滤波器视为基本过滤器和可靠性项的元素乘积³⁰。Dai等人提出了一种自适应空间约束相关滤波算法³¹，以优化滤波器权重和空间约束矩阵。此外，Goutam等人利用了深层和浅层特征的互补特性³²，以提高鲁棒性和准确性。他们的工作在释放深度特征跟踪的潜力方面发挥了重要作用。最近，一些方法试图将基于深度学习的提议网络与相关滤波器跟踪相结合。例如，杨等人提出了一种新颖的长期相关滤波跟踪方法，该方法以协作的方式应用了基于DCF的跟踪模型和新型的目标感知探测器。在他们的方法中，他们根据增强的PSR评估了跟踪结果的可靠性，并使用了基于区域提议网络（RPN, Region Proposal Network）检测器，以在跟踪失败下执行对象检测。Yan等人提出了一个新颖的实时长期跟踪框架³³，该框架基于所提出的粗略模块和精细模块。细读模块旨在使用离线训练的回归模型和验证网络在本地搜索区域中精确定位跟踪对象。略读模块着重于从密集采样的滑动窗口中有效选择最有可能的区域。

研究的主要内容、难点及技术路线

对于国内外研究在目标跟踪算法上的现状和面临的挑战，本文介绍了相关滤波的基本理论并给出了公式推导，在此基础上进一步分析了这种传统相关滤波算法的不足之处，并在其框架之上做了进一步的设计和改进。

主要内容

针对 DSST 算法在模板更新频率单一固定的问题，本文设计了一种基于自适应模板更新的目标跟踪算法。该算法通过检测每一帧图像的PSR峰值强度，从而可以得到关于响应图中响应值的聚集程度信息。PSR的值越大，响应值的聚集程度越高，那么跟踪结果越准确；相反，PSR的值越小，跟踪结果越差。于是我们以PSR的变化来作为评判目标模板更新的依据。根据实验结果表明，改进后的算法对跟踪过程中目标发生尺度变化、光照变化、运动模糊、遮挡、旋转、超出边界等情况时具有较好鲁棒性，与原算法相比，精度提高了16.92%，成功率提高了11.02%。

重点和难点

理解DSST算法的原理和实现方法，并在该基础上对其进行设计和改进。在使用PSR对DSST算法进行补充时，关键在于图像的峰值旁瓣比检测和目标模板的更新。当峰值旁瓣比大于某个值时目标模板不更新，小于某个值时目标模板更新。例如，当目标发生遮挡时，该时间段捕获的图像帧的峰值旁瓣比会降至7以下，此时让DSST算法停止更新模板；当检测到峰值大于7时，则以目标新位置为中心更新模板，这样就可以让算法达到一个良好的跟踪效果。

技术路线

首先了解相关滤波算法和PSR原理，然后使用DSST算法对目标进行快速检测和尺度估计，并得出目标区域的响应值，有利于制定相应的改进措施。在DSST算法里引入PSR判决条件后，使DSST算法准确更新目标模板，达到良好的追踪效果。最后，我们使用改进后的DSST算法与原版算法做对比试验，并对数据集进行整体性能评估。

---

第二章 相关滤波理论与性能评价方法

引言

Blome等人在2010年提出了MOSSE算法之后，因为其出色的跟踪速度相关滤波类算法吸引了众多研究学者。本章重点介绍其跟踪原理，其中主要对核相关滤波跟踪算法的样本的循环位移、核技巧的求解和分类器训练以及目标检测和模板更新方式进行阐述。

相关滤波理论概述

相关滤波跟踪概念

“相关”这个概念来自信号处理领域，我们假设有两个信号 $f$ 和 $g$ ，那它们的相关性可以用公式表示为：

$$(f \otimes g)(\tau)=\int_{-\infty}^{\infty} f^{*}(t) g(t+\tau) d t \tag{2-1}$$

式(2-1)中， $\otimes$ 表示卷积运算，其中 $f^{*}$ 表示 $f$ 的复共轭，信号 $f$ 和 $g$ 我们可以看作是两个函数，两个信号的相似程度越高，那么由公式计算得到的相关值也就越高。我们可以把上式转换一下，这样能提高运算速度，如下所示：

$$F(f \otimes h)=F(f) \odot F(h)^{*}=F(g) \tag{2-2}$$

在上个式中， $F$ 表示傅里叶变换，符号 $\odot$ 表示滤波器模板元素和图像信号之间的相乘运算， $F(h)^{*}$ 表示 $F(h)$ 的复共轭，我们还可以将式(2-2)的简写形式表示如下：

$$F \odot H^{*}=G \tag{2-3}$$

在跟踪过程中运动目标的外观可能会不断地发生变化，我们可以选择 $i$ 个含有目标的图像作为样本，这样尽可能一定程度上提高算法的泛化能力，增强鲁棒性。所以我们把滤波器的目标模板还可以表示为：

$$H_{i}^{*}=\frac{G_{i}}{F_{i}} \tag{2-4}$$

我们可以根据线性回归理论得知，只要知道期望输出的平方和误差以及最小化的卷积运算结果，就能通过训练输入的图像信号来得到滤波器模板，用目标函数表示如下：

$$\min \sum_{i}\left|F_{i} \odot H^{*}-G_{i}\right|^{2} \tag{2-5}$$

通过计算可以得到的一个关于滤波器模板的封闭解，结果表示如下：

$$H^{*}=\frac{\sum_{i}G_{i}\odot F_{i}^{*}}{\sum_{i}F\odot_{i}F_{i}^{*}} \tag{2-6}$$

在这个式子中，我们训练得到滤波器模板 $H^{*}$ 。得到滤波器模板后，我们只需要将模板和帧图像进行一系列相关操作，其中响应最大的点所对应的坐标就可以作为目标区域的估计位置，即获得响应结果。通过这一系列流程，我们实现了模板跟踪中最为关键的相关滤波思想的运用。

循环矩阵

通过循环移位所采集的实验样本，与密集采样得到的实验样本大多较为相似。通过循环矩阵，我们还可以将脊回归算法与信号处理两者相结合，大幅提升对分类器进行训练的速度。循环移位在表示目标图像空间连续变换的建模中发挥了非常重要的价值。在本次研究中，我们把输入信号作为一维单通道样本，同时对循环矩阵的运用机理在视觉目标追踪中进行阐述，得出的结论也适用于观测二维图像实验样本的情况。

用向量 $X=[x_1,x_2,x_3,\ldots,x_n]^T$ 来表示基础实验样本，我们可以将其解释为目标二维图像的垂直或水平展开。然后通过多次循环位移对基础实验样本进行样本变换，即可获得一系列新的样本。将这些大量的实验样本巧妙地组合起来，就得到了我们想要的循环矩阵。要想完成向量 $X$ 准确的循环移位操作，我们可以定义变换矩阵 $P$ 来完成，这样能够使 $X$ 循环移位一个元素，其中置换矩阵形式如下：

$$P=\left[\begin{array}{ccccc} 0 & 0 & 0 & \ldots & 1 \\ 1 & 0 & 0 & \ldots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 & 0 \end{array}\right] \tag{2-7}$$

利用向量 $X$ 我们得到循环矩阵 $Q$ 为：

$$X=C(x)=\left[\begin{array}{ccccc} x_{1} & x_{2} & x_{3} & \ldots & x_{n} \\ x_{n} & x_{1} & x_{2} & \ldots & x_{n-1} \\ x_{n-1} & x_{n} & x_{1} & \cdots & x_{n 2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{2} & x_{3} & x_{4} & \cdots & x_{1} \end{array}\right] \tag{2-8}$$

向量 $X$ 与循环位移操作符 $P$ 相乘得到：

$$P x=\left[x_{1}, x_{2}, x_{3}, \ldots, x_{n}\right]^{T} \tag{2-9}$$

这样我们就实现了将向量 $X$ 向右移动了1个元素，如果把 $X$ 与矩阵 $P$ 的 $u$ 次幂相乘，就相当于把向量 $X$ 向右移动了 $u$ 个元素（ $u$ 为整数）。这样，我们要实现向量 $X$ 任意元素的循环移位只需要改变 $u$ 的值就可以，若 $u \lt 0$ ，向量 $X$ 则向左移动了 $u$ 个元素。因为循环移位操作符 $P$ 为 $n \times n$ 矩阵，说明只有 $n$ 个移位是不重复的。那么，以向量 $X$ 为基础数据样本，通过多次循环移位能够得到的数据样本全集为：

$$\left\{P^{u} x \mid u=0,1,2, \ldots, n-1\right\} \tag{2-10}$$

通过变换矩阵 $P^{u}$ ， $C(x)$ 可表示为：

$$C(x)=\left[\begin{array}{c} \left(P^{0} x\right)^{T} \\ \left(P^{1} x\right)^{T} \\ \left(P^{2} x\right)^{T} \\ \cdots \\ \left(P^{n-1} x\right)^{T} \end{array}\right] \tag{2-11}$$

循环矩阵的性质包括傅里叶变换对角化，通过对该性质的运用，能够进一步降低运算量。该性质用公式可表示为：

$$X=F \operatorname{diag}(\hat{x}) F^{H} \tag{2-12}$$

上面这个式子中， $X$ 是通过循环移位产生的循环矩阵，代表向量 $X$ ， $F$ 为一个常量矩阵，代表傅里叶变换矩阵， $\operatorname{diag}(\cdot)$ 是取对角化的操作符， $\hat{x}$ 代表 $X$ 的傅里叶变换。因为离散傅里叶变换，我们可以借助常量矩阵 $F$ 通过计算得到任一向量 $Z$ 的离散傅里叶变换：

$$F(z)=\sqrt{n}Fz \tag{2-13}$$

在 $X^{H}X$ 计算中，我们带入到公式(2-14)，可以得到：

$$X^{H} X=F \operatorname{diag}\left(\hat{x}^{*}\right) F^{H} F \operatorname{diag}(\hat{x}) F^{H} \tag{2-14}$$

因为 $F^{H}F=I$ 所以我们可以把它消掉：

$$X^{H} X=F \operatorname{diag}\left(\hat{x}^{*}\right) \operatorname{diag}(\hat{x}) F^{H} \tag{2-15}$$

又因为 $\operatorname{diag}(\hat{x})$ 和 $\operatorname{diag}(x)$ 两者都是对角矩阵，所以计算可以简化为对角线上的元素相乘，我们可以得到：

$$X^{H} X=F \operatorname{diag}\left(\hat{x}^{*} \cdot \hat{x}\right) F^{H} \tag{2-16}$$

我们将式(2-16)带入到脊回归中去，通过向量的点乘计算和傅里叶变换，有：

$$\begin{aligned} w &=\left(X^{H} X+\lambda I\right) \\ &=F \operatorname{diag}\left(\frac{\hat{x}^{*}}{\hat{x}^{*} \cdot \hat{x}+\lambda}\right) F^{H} y \end{aligned} \tag{2-17}$$

对上面的公式再一次简化，就可以得到如下闭合解：

$$\hat{w}=\frac{\hat{x}^{*} \cdot \hat{y}}{\hat{x}^{*} \cdot \hat{x}+\lambda} \tag{2-18}$$

我们使用这一方法，就可以通过上述样本向量的傅里叶变换以及矩阵的点乘就可以得到目标模板。如果不使用循环移位的操作方法，那么在求解的时候需进行矩阵的乘法运算和求逆，这个运算的复杂度是 $O(n^{*})$ ，我们也可以加入循环矩阵来让复杂度降至 $O(n\log n)$ ，这样就可以保证实时性跟踪。

结合上面的循环样本不难发现，在整个运算过程中我们只需获取一次实验样本的基础信息，而真正所需要的循环移位的样本并未产生，只是在推导过程中使用，所以不需要多余的内存空间来存储实验样本。把循环移位得到的实验样本数据集与快速傅里叶变换相结合，可大大降低运算量。

岭回归模型

目标跟踪算法是通过把前景与背景看作正负样本的二分类问题，然后利用一种岭回归训练分类器，能够达到与支持向量机（SVM）这样复杂的分类器相似的分类效果。

我们假设一列实验样本为 ${x_i,y_i}$ ， $y_i$ 是 $x_i$ 的理论回归期望，通过分类器训练可以得到函数 $f(x)=w^{T}x$ ，并使得损失函数

$$\min _{w} \sum_{i}\left(f\left(x_{i}\right)-y_{i}\right)^{2}+\lambda\|w\|^{2} \tag{2-19}$$

如果要让式子(2-19)取最小值，那么得让实验样本 $x_i$ 的输出 $f(x_i)$ 和回归期望 $y_i$ 的平方差尽量小。在上面式子中， $w$ 是分类器参数，而 $\lambda$ 则是正则化参数，它的作用是防止过拟合。要使得式子最小，求导得：

$$w=\left(X^{T}X + \lambda I\right)^{-1}X^{T}y\tag{2-20}$$

其中 $y$ 表示的是回归目标，而 $X$ 表示的是由实验样本组成的矩阵。

由于复数矩阵，我们可以把式子(2-20)转换成傅里叶域再简化计算，提高计算的效率，其中变化如下：

$$w=\left(X^{H}X + \lambda I\right)^{-1}X^{H}y\tag{2-21}$$

其中，$X^{H}$ 和 $X$ 两者之间是复共轭转置矩阵关系。

核空间岭回归模型

我们常用的回归分析方法一般是用数理统计的方法来进行分析数据的，首先要建立因变量和自变量之间的理想回归模型，最终达到预测因变量的变化。其中最经典的就是Hoerl和Kennard两位学者共同提出的岭回归算法。所谓的岭回归算法，就是把正则项引入到最小二乘法的基础上，这样可以让回归模型拥有良好的泛化能力及稳定性，然而就算是岭回归算法也不能处理一些情况，比如自变量间非线性相关。如果我们在岭回归算法基础的上引进核方法，就可以得到核脊回归算法（KRR, Kernel Ridge Regression），而自变量空间就可以通过核函数来被映射到高维特征空间里，再用上面的岭回归方法分析和处理高维特征空间中的数据。

也就是说，核岭回归其本质是使用岭回归来做预测，是回归算法的一种。岭回归的作用是做线性回归，它可以拟合出一条直线，也可以通过增加一个核函数来面对非线性情况，同样将自变量空间映射到高维特征空间。最后在高维特征空间里同样可以做线性回归。例如：

$$y=f(x)\tag{2-22}$$

式(2-22)中， $y$ 为因变量，矩阵 $x$ 为多维辅助变量；同时 $y$ 也可以换成函数的形式，例如：

$$f(x)=\sum_{i=1}^{n}w_{n}\phi_{n}\left(x\right)\tag{2-23}$$ $$f(x)=\sum_{i}\alpha_{i}K\left(x_{i},x\right)\tag{2-24}$$

式(2-24)中，核函数 $K(x_{i},x)$ 定义为：

$$K\left(x_{i},x\right)=\sum_{n}\phi_{n}\left(x_{i}\right)\phi_{n}\left(x\right)\tag{2-25}$$

核函数确定后，再通过岭回归算法来解对偶变量 $\alpha_{i}$ ，改良岭回归描述如下：

$$\min \lambda \sum_{n} w_{n}^{2}+\sum_{n} \zeta_{n}^{2}, \text { s.t. } y_{i}-\lambda \sum_{n} w_{n} \phi_{n}\left(x_{i}\right)=\zeta_{i}\tag{2-26}$$

式(2-26)中， $\lambda$ 是岭参数是用来控制岭回归的正规化度，应用数学运算可以证明公式(2-24)中对偶变量 $\alpha_{i}$ 可以表示为：

$$\alpha_{i}=\sum_{j}\left(K + \lambda I\right)_{ij}^{-1}y_{i}\tag{2-27}$$

高斯核函数（RBF, Radial Basis Function），是我们最常用的核函数：

$$K_{i j}=K\left(x_{i}, x_{j}\right)=\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}\right)\tag{2-28}$$

式(2-28)中， $\sigma$ 是高斯核带宽，用来控制径向作用范围； $x_j$ 为核函数中心，而 $\left|x_i - x_j\right|^2$ 则表示的是向量 $x_i$ 和向量 $x_j$ 的欧氏距离，随着两个向量的距离增大，高斯核函数单调递减。

公共数据集与评估方法

在进行有关图像跟踪实验时，我们需要用到很多数据集来做一种基准测试，并且这些数据集几乎涵盖了所有现实生活中在进行图像跟踪时可能遇到的情景，这样可以让人更直观地看到不同算法之间的表现。

常用公共数据集

在计算机视觉领域，我们常用的公共数据集有两种；一是OTB100，二是TColor-128。OTB100这里面涉及到100个视频序列，涵盖了当前图像跟踪中最普遍的问题，比如低分辨率和背景干扰，以及目标遮挡和快速运动、平面内旋转和平面外旋转等。并且这一目标跟踪基准数据集多达11中挑战因素，包括照明变化（IV）、尺度变化（SV）、遮挡（OCC）、变形（DEF）、运动模糊（MB）、快速运动（FM）、平面旋转（IPR）、平面外旋转（OPR），视图（OV），背景剪切（BC）和低分辨率（LR），如表2-1所示。它的权威性和可靠性也得到学术界的认可，并普遍投入到目标跟踪算法的测试当中，形成了众多目标跟踪算法的测试标准。

表2-1 OTB100数据集中11种属性

属性列表	属性描述	代表视频序列
光照变化	目标区域光照明显变化	Car4, CarDark, David
尺度变化	首帧与当前帧的边框之比超过两倍	CarScale, Dog1, Singer1
遮挡	目标部分或完全被遮住	Jogging1, Jogging2
形状变化	非刚性的目标形变	Basketball, Bird1
运动模糊	由于目标或摄像头的移动，导致目标区域的模糊	Biker, BlurBody
快速运动	目标帧间位移超过20个像素	Bird1, DragonBaby
面内旋转	目标在图像平面内旋转	Bird2, Dancer
面外旋转	目标旋转出图像平面	Box, Boy
脱离视野	目标的某些部分离开了视图	Dudek, Human6
背景干扰	目标附近的背景具有与之相似的颜色或纹理	Crowds, David3, Deer
低分辨率	目标区域少于400个像素	Skiing, Surfer, Walking

第二种也是本文所用的数据集TColor-128，其中包含的视频序列更多，并且该数据集由两部分构成。第一部分包含了50个经常测试的颜色序列，但是这些序列还不完全可以彻底评估颜色跟踪器。一方面，由于视觉跟踪中涉及到大量因素和视觉跟踪器中的许多可调参数，因此对50个序列的实验可能不足以得出显著的结论。另一方面，由于这些序列在先前的研究中的普及，它们的性能通常接近饱和，并且其中许多并不像最初看起来一样困难。这两个观察结果激发了学者收集更多的颜色序列，这就构成了TColor-128的第二部分。

Tcolor-128的第二部分包含从互联网重新收集的78个颜色序列。通过设计，78个序列在很大程度上增加了前50个序列的多样性和挑战性，并涉及各种情况：例如高速公路、机场航站楼、火车站、音乐会等，这些序列具有许多挑战因素，例如完全靶标的较大的照明变化，显着的目标变形和低分辨率。

除了地面目标跟踪外，TColor-128中的每个序列还有其它挑战因素，该数据集同样使用了上面提到的11个因素。其中，当目前框架中边界框的大小与第一帧的大小之比落在范围 内时，为尺度变化；当目标运动大于20像素时，为快速运动；当地面目标跟踪框内的像素数量少于400时，则是低分辨率。图2-1给出了Tcolor-128中挑战因素的分布。

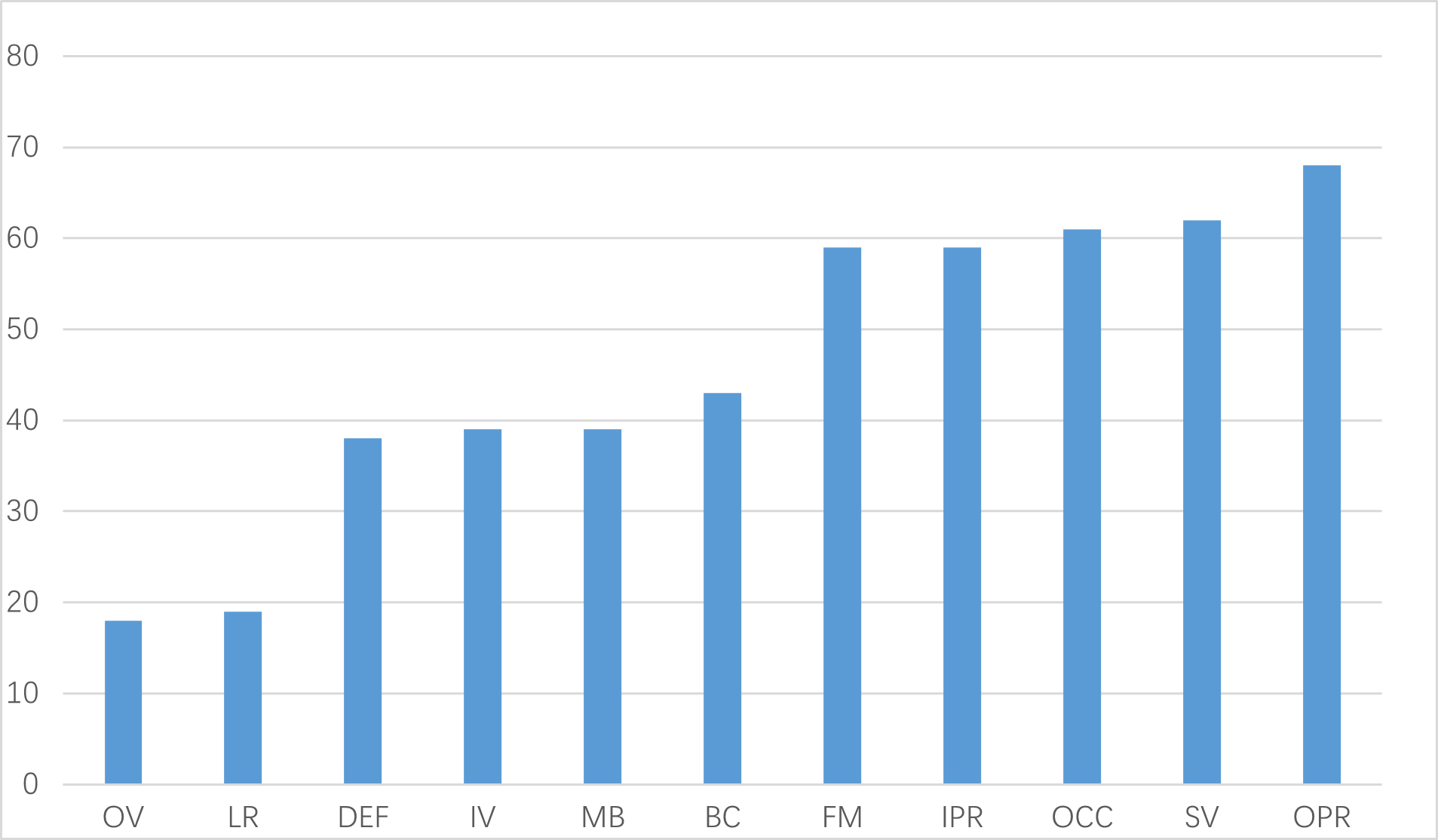
图2-1 TColor-128中挑战因素的分布

性能评估方法

我们主要通过两个评价指标来评估算法的整体跟踪性能：

• 距离精度

距离精度表示的是关于真实目标跟踪框和预测目标跟踪框两者中心的平均欧式距离，值越小跟踪越精确。中心位置误差计算方式如下：

$$P=\sqrt{\left(X_{A}-X_{B}\right)^{2}+\left(Y_{A}-Y_{B}\right)^{2}}\tag{2-29}$$

式(2-29)中 $P$ 表示的是中心位置的误差值，我们以蓝色矩形表示实际目标跟踪框，橙色矩形表示预测目标跟踪框的，A、B分别表示两个矩形框的中心，如图2-2所示：

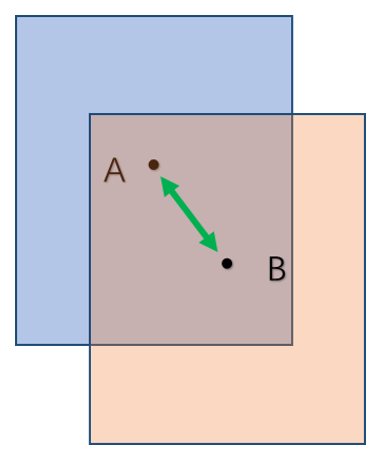
图2-2 中心位置误差示意图

• 成功率曲线

当丢失跟踪目标时，不能准确预测目标位置，所得到的信息是随机的，这时不能够合理的通过中心位置误差对跟踪性能评估。为了更好地评价每个跟踪算法的性能，我们可以采用更为准确和严谨的精度图曲线。对于给定的位置误差阈值为 $20pixels$ ，精度曲线图表示在一个视频序列中，中心位置误差满足要求的图像帧数占总数的百分比。

成功率用重叠率进行衡量，定义重叠率为：

$$S=\frac{\operatorname{Area}\left(B_{t} \cap B_{a}\right)}{\operatorname{Area}\left(B_{t} \cup B_{a}\right)}\tag{2-30}$$

$B_a$ 表示目标实际的边界框， $B_t$ 表示目标跟踪的边界框， $\cap$ 和 $\cup$ 分别表示两个边界框内区域的交集和并集，成功率表示重叠率 $S$ 大于给定阈值的图像帧数占总图像帧数的百分比，我们可以将成功率图曲线下的面积 $(A\cup C)$ 作为评价标准。重叠区域示意图如图2-3，蓝色方框表示目标的实际边框，黄色方框表示预测的目标边框，中间黄色部分表示两个边框的重叠区域。

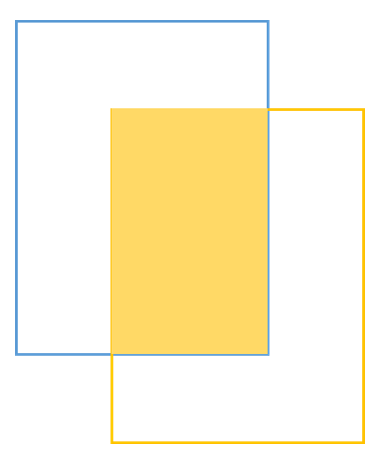
重叠区域示意图

本章小结

本章首先重点介绍了相关滤波理论，主要说明了核相关滤波算法的原理和步骤，通过岭回归分类器来训练目标滤波器模板，得到核相关滤波器，其中可以由循环位移操作获取训练所需的样本。而循环矩阵和傅里叶变换的性质极大的提高了计算的效率，并且利用核函数技巧对滤波器进行求解所得的相关滤波器，对目标的位置预测更加准确。然后介绍了两种常用的公共数据集，并对本文实验中采用的数据集TColor-128进行了充分地阐述。

---

第三章 基于自适应模型更新的目标跟踪算法

引言

在跟踪过程中，目标的外形并非一直保持不变，要想维持跟踪器的精度，只有持续地更新目标模板。但是传统的DSST算法在目标模板更新时，频率单一固定，由于遮挡的影响，复杂的背景会导致目标模板与不相干的区域匹配，而目标区域的相似性也会大大降低，因此目标的遮挡是一个急待解决的问题。更严重的是，如果使用错误的信息更新模板，那么将直接导致目标跟踪失败，因为此时的模板已受到污染。此外，运动速度过快、运动模糊、形变等其他因素也可能导致跟踪器漂移。所以，为了增强跟踪器在复杂情景中的鲁棒性，我们在设计跟踪算法时要考虑到各种情形。

为了解决上述问题，我们在原算法的基础上引进了一个新的参考变量PSR来决定目标模板是否应该更新，并将改进后的算法与另外几类进行对比。实验结果显示，相较于原本的DSST算法，改进后的在抗干扰、抗遮挡这方面的效果有了显著提升。

PSR判据

PSR的作用主要是用于测量峰值强度，依靠该峰值强度我们可以得到关于响应图中响应值的聚集程度信息。PSR的值越大，响应值的聚集程度越高，那么跟踪结果越准确。在响应图中，PSR的计算依靠最大峰值和峰周围 窗口的像素，根据相关定义，PSR可以表示为

$$PSR=\frac {g_{max} - \mu_{s1}}{\sigma_{s1}}\tag{3-1}$$

式子(3-1)中， $g_max$ 是最大的峰值， $\sigma_s1$ 是标准差， $\mu_s1$ 是旁瓣平均值。通过多次测试，正常运行时的跟踪器，PSR取值通常分布在 $[20.0,60.0]$ 之间。但是，当目标丢失或发生遮挡时，PSR的值一般就会下降到7.0以下。因为PSR对遮挡比较敏感，所以该参量可以判断目标是否被遮挡。

目标快速检测

DSST算法的创始人Martin将两个独立的相关滤波器应用到实际代码中，主要作用是分别对目标的尺度和位置进行评估。以 $1\in{1,\ldots,d}$ 表示改变特征后的维度数，这一算法中可以把HOG、CN和灰度特征等进行融合，考虑到实际情况我们选用HOG特征，并得到最小均方误差和公式为：

$$\varepsilon=\left\|\sum_{l=1}^{d}h^{l}\ast f^{l} - g \right\|^{2} + \lambda \sum_{l=1}^{d}\left\|h^{l} \right\|^{2}\tag{3-2}$$

在公式(3-2)中， $f$ 为特征， $f^{l}$ 代表的是 $d$ 维特征 $f$ 的第l维； $d$ 代表的是对 $f$ 进行多次训练后获取的较为理想的输出， $h$ 代表的是相关滤波器； $\lambda$ 代表的是正则项系数，可以用来消除 $f$ 频谱中的零频分量的影响。一般在考虑1个训练样本的情况下，可得到：

$$H^{l}=\frac {\overline G F^{l}}{\sum_{K=1}^{d}\overline {F^{k}}F^{l} + \lambda}=\frac{A_{t}^{l}}{B_{t}}\tag{3-3}$$

式(3-3)中， $G$ 代表的是较为符合的高斯分布的形状。要求解 $d\times d$ 维线性方程比较繁琐，为了计算的便利性，以 $B_t$ 和 $A_t^l$ 分别代表 $H^l$ 的分母和分子部分，然后分别进行迭代更新，其具体公式为：

$$A_{t}^{l}=\left(1- \eta \right)A_{t - 1}^{l} + \eta \overline {G_{t}^{l}}F_{t}^{l}\tag{3-4}$$ $$B_{t}=\left(1 - \eta \right)B_{t - 1}^{l} + \eta \sum _{k = 1}^{d} \overline{F_{t}^{k}}F_{t}^{k}\tag{3-5}$$

式(3-4)和(3-5)中， $\eta$ 代表的是学习率，对于一帧新的图像 $Z$ ，它的响应得分为 $y$ ，可以得到：

$$y=F^{-1}\left\{\frac{\sum_{k=1}^{d} \overline{A^{l}}Z^{l}}{B+\lambda} \right\}\tag{3-6}$$

其中，当 $y$ 的数值是最大的位置时，就是对新目标位置的估计。

DSST算法与KCF算法以及MOSSE算法相比，最显而易见的优势就是可以通过对尺度和位置的分开计算，从而快速准确地实现对尺度的估计。因为该算法有两个相关滤波器，首先该算法利用目标位置滤波器对确定新位置，然后通过尺度滤波器，把当前中心位置作为中心点可以得到不同尺度的候选块，从而找到最好的匹配尺度。

我们假设 $R$ 为目标框的高度，而 $P$ 是目标框的宽度，那么当前目标帧的大小则是 $P\times R$ ，以 $a$ 表示尺度因子 $S$ 为尺度，以目标的原有视觉位置为中心选取的图像候选块的大小为：

$$a^{n}P\times a^{n}R, n\in \left\{\left[-\frac{s-1}{2},\ldots ,\frac{s-1}{2} \right] \right\}\tag{3-7}$$

我们先确定目标新位置信息，在该算法中以刚才的位置信息为基础来确定尺度信息，所以在持续的两帧图像中，尺度的变化量一般小于位置的变化量。HOG特征在位置滤波器中能够获取的cell尺寸为 $1\times 1$ ，和 $2\times 2$ 的block尺寸，如果cell尺寸 $4\times 4$ ，block尺寸 $2\times 2$ ，那么这是尺度滤波器。在获取候选框的HOG特征时，我们采取了33种不同的尺度。并且还得将得到的特征与汉明窗相乘，这样可以消除傅里叶变换可能对结果造成的影响。

目标模型自适应更新

我们采用DSST算法来更新目标模板的原理是，检测当前图像的峰值旁瓣比是否小于给定阈值；当峰值旁瓣比大于7时，说明目标没有受到遮挡，此时模板更新，如公式(3-8)所示：

$$\left\{\begin{array}{l} A_{t}^{l}=(1-\eta)A_{t-1}^{l}+\eta \bar{G}_{t}F_{t}^{l}\\[2ex] B_{t}=(1-\eta)B_{t-1}+\eta \sum_{k=1}^{d}\bar{F}_{t}^{k}F_{t}^{k} \end{array}\quad,PSR>7,\eta \neq 0.\right.\tag{3-8}$$

当峰值旁瓣比小于7时，说明目标受到了遮挡，此时模板不更新，如公式(3-9)所示。通过图3-1我们可以明显看到，当目标处于第35帧图像中时没有受到遮挡，此时PSR远大于7，模板可以更新；当目标处于第45帧图像中时开始受到遮挡，且PSR远小于7，此时模板不再更新，直到第65帧时目标脱离了遮挡，PSR大于7，模板继续更新。

$$\left\{\begin{array}{l} A_{t}^{l}=A_{t-1}^{l} \\[2ex] B_{t}=B_{t-1} \end{array} \quad, PSR \leq 7, \eta=0 .\right.\tag{3-9}$$

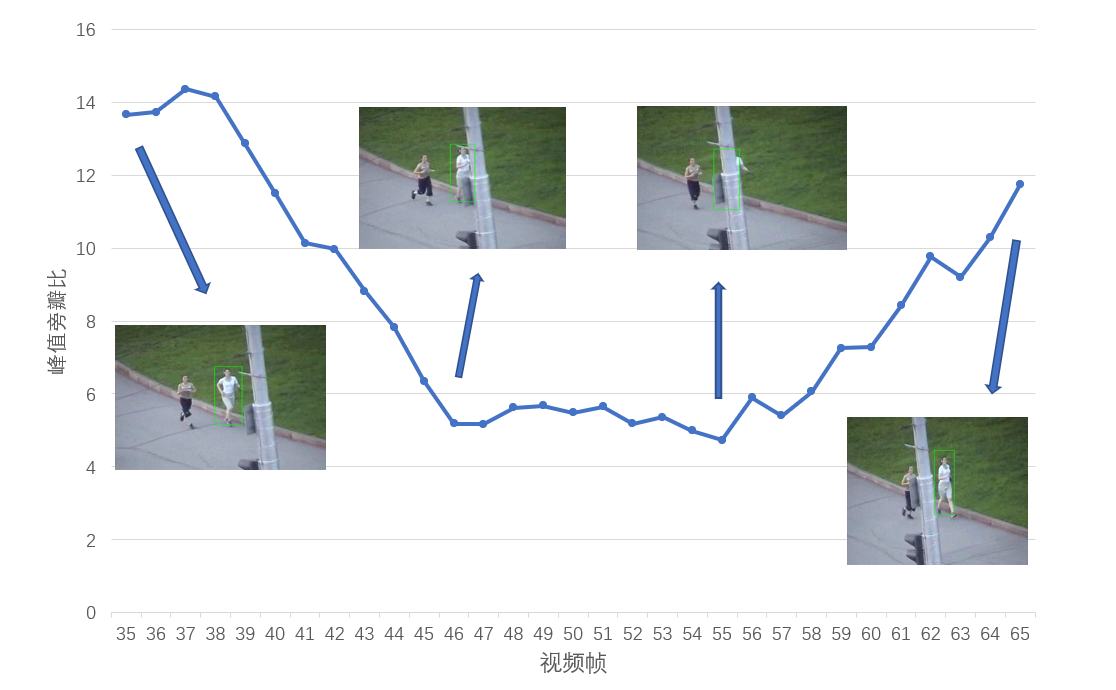
Jogging2视频序列中的遮挡实验

算法流程描述

DSST是由位置滤波器和尺度滤波器两部分构成的，在一个完整的流程中，首先输入首帧图像初始化参数。我们通过位置滤波器以目标旧位置为中心采集样本，计算并得到样本的像素点特征，然后乘以ham窗作为测试输入。因为加入了PSR判决条件，这里会判断当前帧的峰值旁瓣比是否满足我们预设条件，当PSR大于阈值时更新目标模板，小于时就不更新。后面通过尺度滤波器进行尺度样本提取，如果目标模板更新了，就以新位置为中心提取样本，如果没有更新则以旧位置提取样本。根据样本我们可以提取到HOG特征，最后再乘以ham输出图像。整个实验流程如图3-2所示：

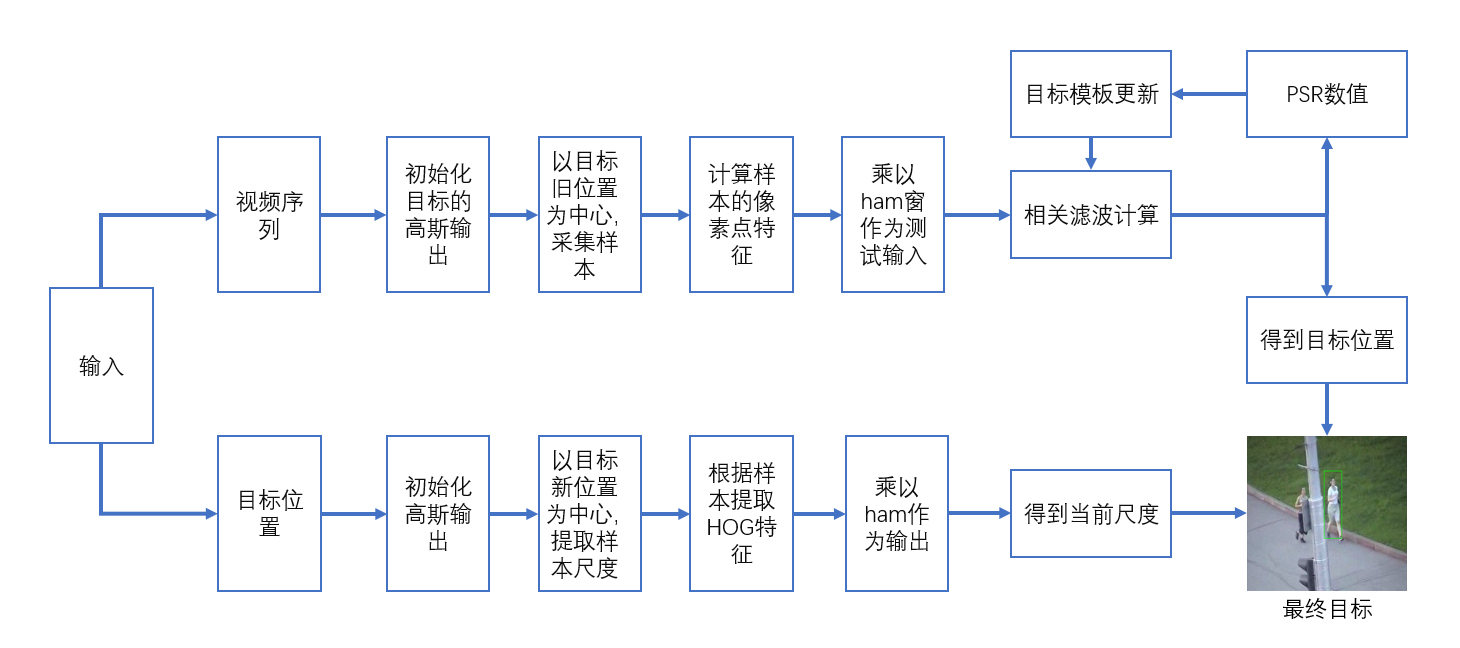
DSST算法模板更新流程图

本章小结

本章内容主要介绍了DSST算法的公式和原理以及在目标追踪和模板更新里的运用，为了解决该算法本身的不足之处，我们又引入了峰值旁瓣比和PSR判决的概念，并且，在PSR的介入下，我们改进了目标检测和模板更新的流程，让DSST算法发挥出更优秀的表现。

---

第四章 实验结果与分析

引言

前面我们大致介绍了相关滤波原理和DSST算法，并分析了DDST算法在自适应更新方面的已知问题，然后我们通过峰值旁瓣比在现有基础上进行了改进。改进后的DSST算法理论上在改善模板被噪声污染方面上有了更显著的效果。这里我们用TColor-128公共数据集来实际验证改进后的算法是否达到我们的期望，以及和原来的算法之间的差别。本章内容涵盖了以下几个方面：实验环境配置、算法效果对比、总体评估和定性评估。

主要参数与实验环境设置

我的实验硬件环境为Intel Core i5-8265U CPU，主频 2.1GHz，最大睿频3.4GHz，内存8GB，软件环境为MATLAB R2016a，OPENCV3.5，TDM-GCC MinGW-w64。为验证改进的DSST算法的可行性，将其与SAMF、FCT、KCF 、MEEM、MIL和L1APG六种算法以及原本的DSST 算法在TColor-128数据集上进行对比实验。实验中的参数保持一致。

消融实验

为了验证改进后的DSST算法的实际效果，我们将该算法与原来算法的跟踪器，通过TColor-128数据集来做总体性能评估。

Precision plots表示的含义是：跟踪算法估计的目标位置（bounding box）的中心点与人工标注（ground-truth）的目标中心点，这两者的距离小于给定阈值的视频帧的百分比，不同的阈值得到的百分比也不一样，因此可以获得一条曲线。而Success plots表示的含义是：首先定义重合率得分（overlap score, OS），追踪算法得到的目标位置（记为 $a$ ）与人工标注的（记为 $b$ ），重合率定义为 $OS=\frac{\left|a\cap b \right|}{\left|a\cup b \right|}$ ， $|\cdot|$ 表示区域的像素数目，当某一帧的 $OS$ 大于所给的阈值时，该帧视为成功（Success），总的成功帧占所有帧的百分比就是成功率（Success rate）， $OS$ 的取值范围为 $[0,1]$ ，阈值设定为0.5，因此可以绘制出一条曲线。

通过精确度曲线图4-1可以看出，在给定阈值条件下，原DSST算法在精确度方面与改进后的算法明显相差16.92%；在成功率方面则相差11.02%。由此可见，改进后的效果提升很明显。

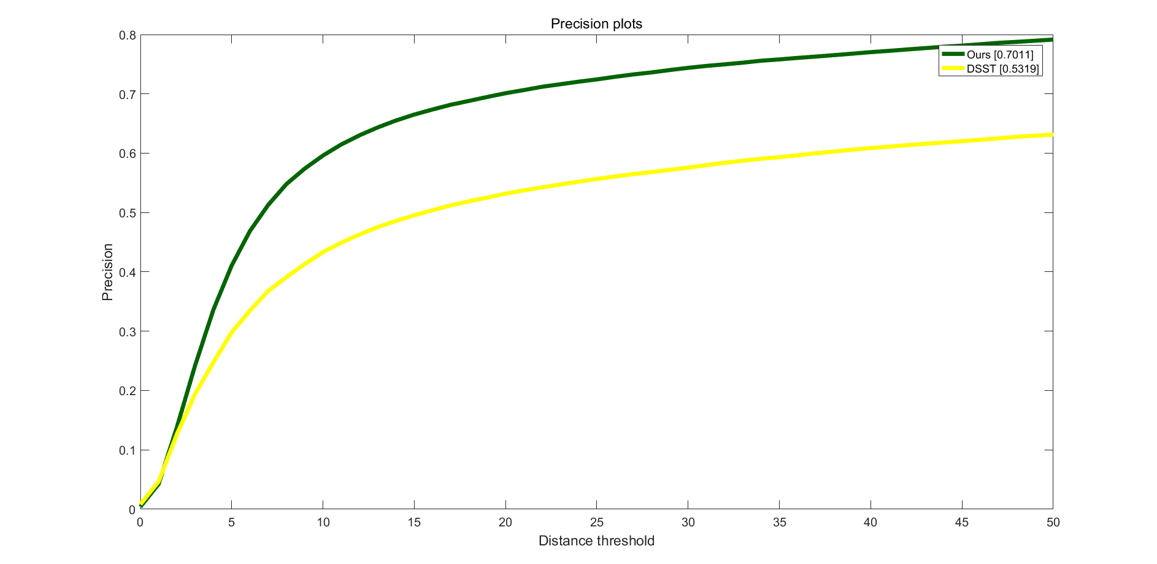
图4-1 改进后的算法与原算法的精确度曲线

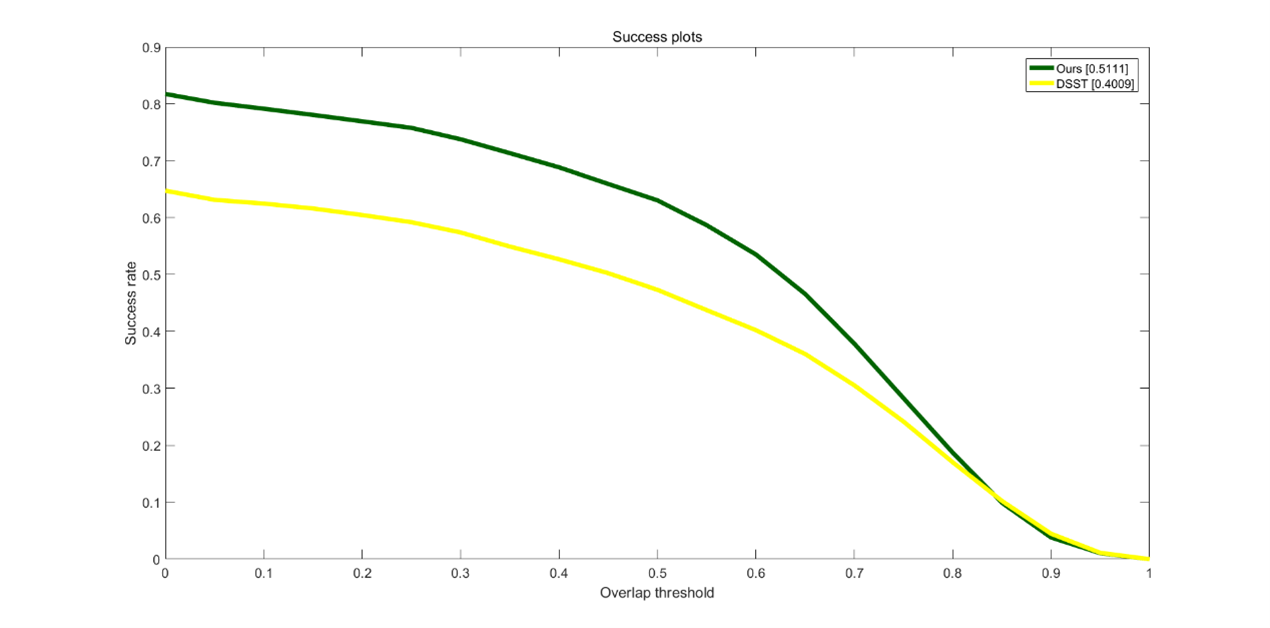
图4-2 改进后的算法与原算法的成功率曲线

整体性能评估

我们先用原DSST算法来和其他六种跟踪器进行性能评估，通过图4-3我们可以很明显地看出来，在相同阈值下，原DSST算法的百分比明显小于其他的算法。同样，在图4-4中我们可以看出在相同阈值下，原DSST算法的成功率很低，远不如其他算法。

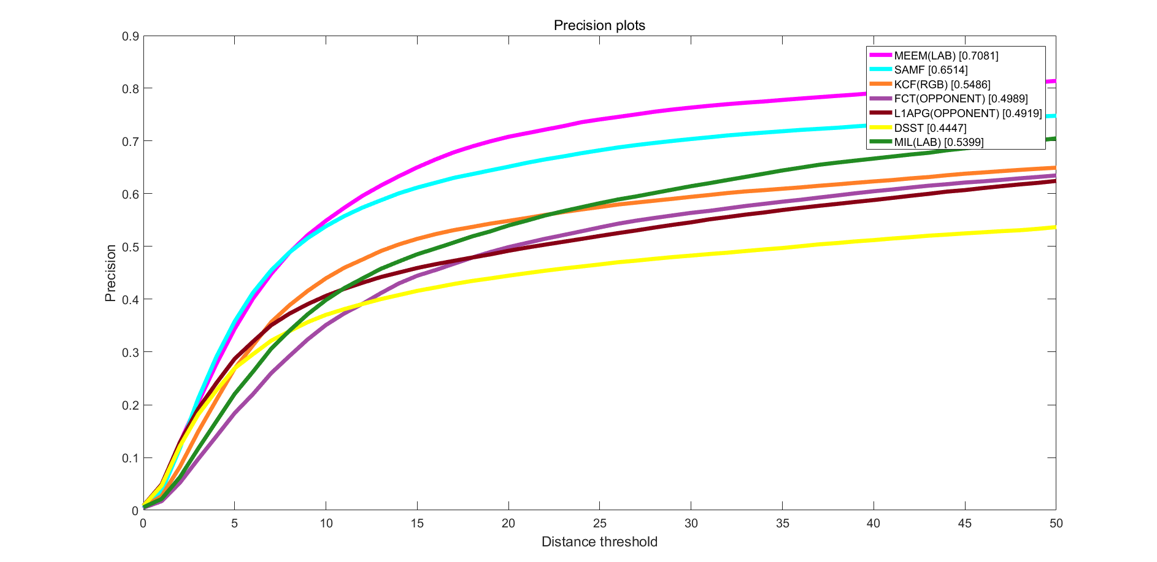
图4-3 DSST的精确度曲线

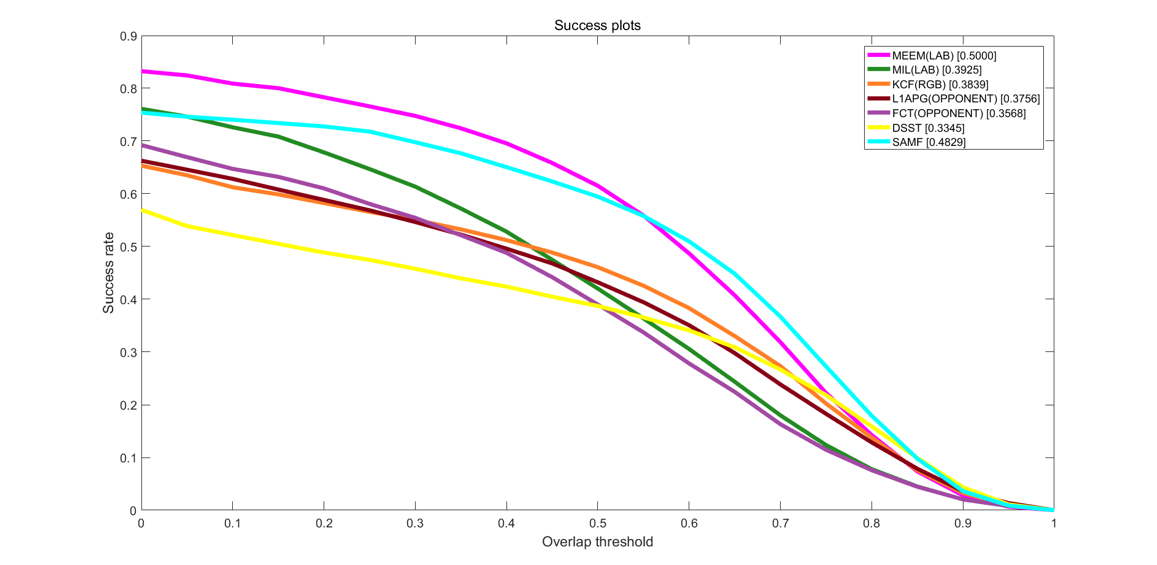
图4-4 DSST的成功率曲线

现在，我们再来观察改进后的DSST算法在PSR判决下的性能提升。通过图4-5和4-6可以明显看出，在相同的阈值条件下，改进后的算法的性能有显著提升，实验结果达到了我们的期望。

在跟踪精确度上，改进后的算法排在第二位，比第一的MEEM只差0.7%，而远远超出第三名的SAMF的5%；在跟踪成功率上，改进后的算法直接排在第一位，甚至比第二名的高出1.1%，比第三名的SAMF更是高出2.9%。而相较于传统的跟踪器算法比如KCF，在成功率和精确度上分别落下我们12.8%和15.3%，差距显而易见，如表4-1所示。

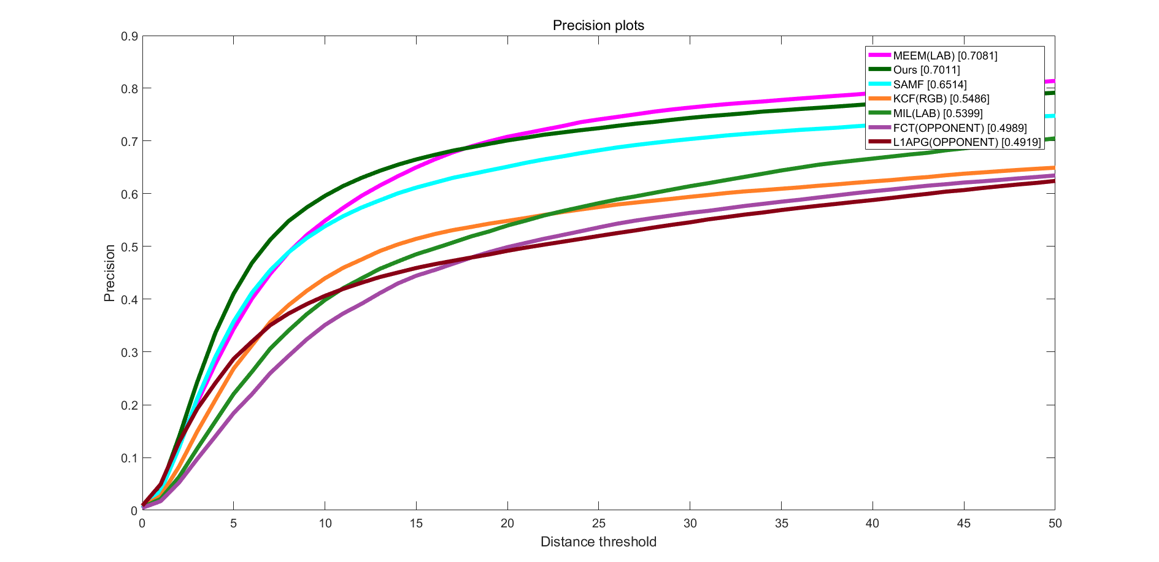
图4-5 DSST_ours的精确度曲线

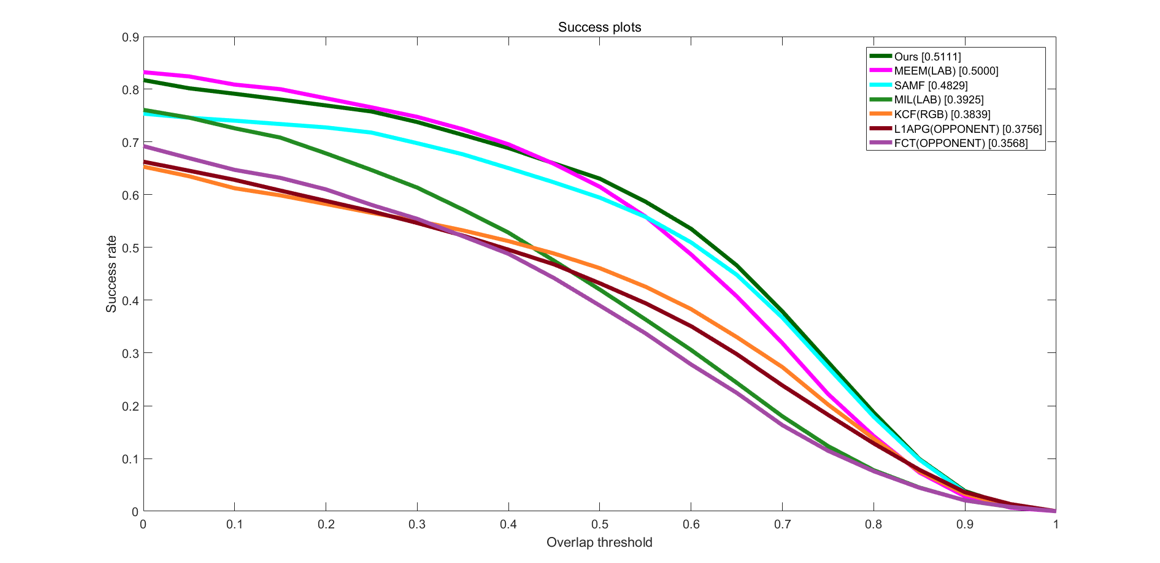
图4-6 DSST_ours的成功率曲线

---

表4-1 7种跟踪器在相同阈值条件下的跟踪成功率和精确度（%）

	Ours	MEEM	SAMF	MIL	KCF	L1APG	FCT
成功率	51.1	50.0	48.2	39.2	38.3	37.5	35.6
精确度	70.1	70.8	65.1	53.9	54.6	49.1	49.8

在上面我们把DSST算法和其他目标跟踪算法分别做了对比试验，因为TColor-128数据集涵盖了多种实际的目标跟踪可能会遇到的干扰因素，比如遮挡、光照、模糊、速度过快等，所以实验对比下来不同的算法的结果都得到了应有的表现。现在我们把所有涉及到的跟踪器都放在一起做一个总的性能评估。可以看到，在图4-8中原DSST算法也是有着不差的成功率，但是在图4-7中的精确度的表现就很差，具体体现在目标跟踪时，该算法对尺度变换、目标遮挡等因素的应对能力较弱。

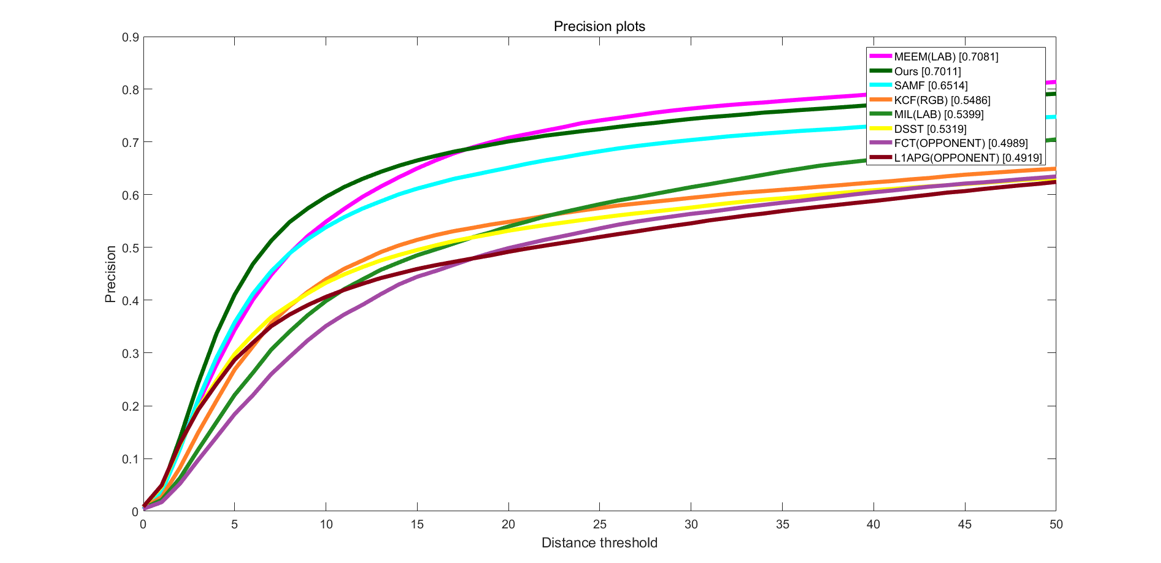
图4-7 8种跟踪器的整体精确度曲线

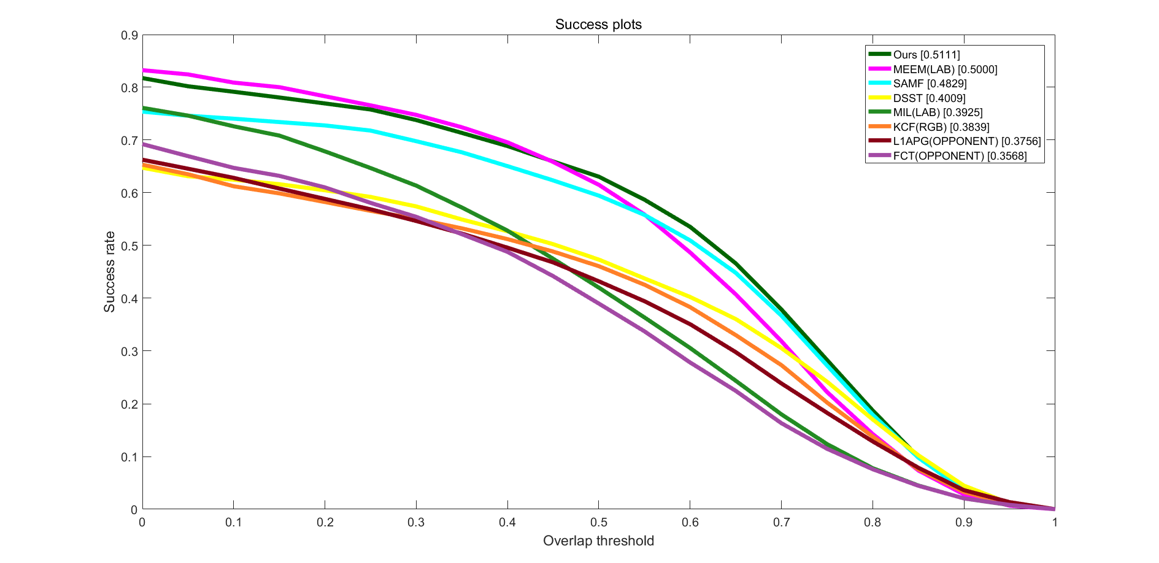
图4-8 8种跟踪器的整体成功率曲线

定性评估

为体现改进后的DSST算法在尺度变化、目标遮挡、超出视野等一系列干扰因素下的目标跟踪性能，我们从众多视频序列中选取了七组比较有代表性的跟踪效果图，将改进的DSST算法和传统的5种跟踪算法进行对比分析。其中Crossing、David2、Jogging1三组视频序列是属于OTB100数据集，Bee_ce、Bicycle、Walking、Woman这四个视频序列是属于TColor-128数据集，每个视频序列的信息如表4-2所示。

表4-2 实验数据集序列信息

视频序列	主要干扰属性	帧数
Bee_ce	快速移动、运动模糊	30
Bicycle	背景复杂	150
Crossing	尺度变换	30
David3	目标遮挡	83
Jogging1	目标遮挡	68
Walking	尺度变换	412
Woman	背景复杂、尺度变换	235

• 快速移动

图4-9是一组快速运动的视频序列，由于目标的快速移动导致图像变得模糊，加大了目标跟踪的难度。在第18帧图中所有的算法都还能准确捕捉到目标，但是在30帧的时候，传统的KCF算法已经脱离了目标，在第41帧的时候，L1APG也脱离了目标包括跟踪性能优秀的MEEM算法，这时我们的算法还能捕捉到目标。在图4-10这组图像中，体现出了显著的鲁棒性。

图4-9 本算法与其他5种算法在Bee_ce视频序列上的跟踪结果对比

• 背景复杂

图4-10是一组背景元素复杂的视频图像，在第10帧时，图中的元素较少，所有的算法都能准确捕捉到目标，但是在第120帧图像中，目标附近出现了几个行人和红绿灯，他们的大小及距离让其中一些算法产生偏离，只是还没有明显脱离。在第150帧图像中，KCF算法已经脱离目标，而其他算法均已产生不同程度的偏差，只有我们的还能完全捕捉到目标位置。在图4-11中的第100帧图像中，由于目标与旁边的汽车走到了一起，此时红色的L1APG算法已经产生明显偏离，在第561帧图像中，KCF和L1APG脱离了目标，只有其余四个还在，这也同样体现出我们的算法的鲁棒性。

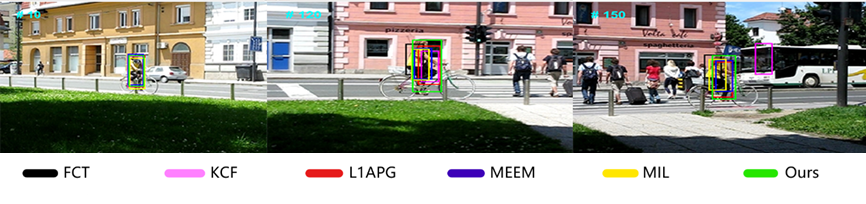
图4-10 本算法与其他5种算法在Bicycle视频序列上的跟踪结果对比

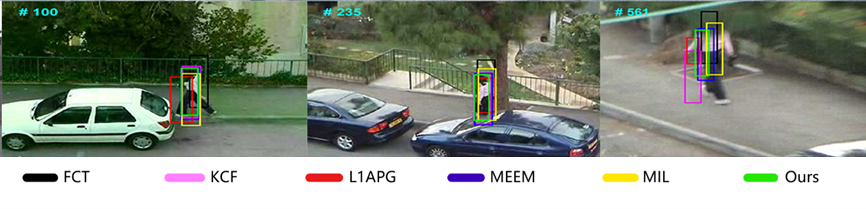
图4-11 本算法与其他5种算法在Woman视频序列上的跟踪结果对比

• 尺度变换

在图4-12中，由于目标从近到远的位移导致了图像中发生了连续的尺度变换，这也是很考验算法的鲁棒性。在第30帧图像中，因为目标的尺寸已经变小，黑色的FCT算法和红色的L1APG算法开始脱离目标，在第111帧图像中这两种算法就完全脱离了，同时KCF、MEEM和MIL算法也产生偏离，只有我们的还能刚好完全捕捉到目标的尺寸。同理，在图4-13的第412帧图像中，其他算法都失去了目标的准确尺寸，但是在PSR判据的帮助下，本文的算法依然还能锁定目标的尺寸。

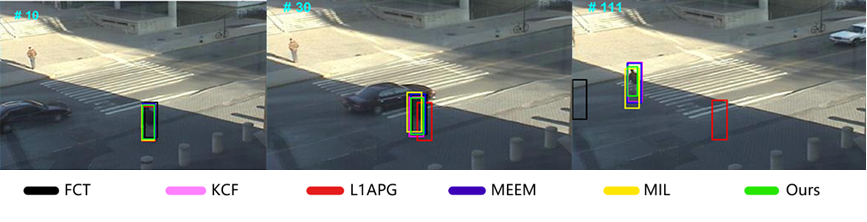
图4-12 本算法与其他5种算法在Crossing视频序列上的跟踪结果对比

图4-13 本算法与其他5种算法在Walking视频序列上的跟踪结果对比

• 目标遮挡

目标遮挡也是一个非常考验算法鲁棒性的问题，很大程度上决定了这个算法能不能作为实际使用。在图4-14中，当目标移动到树的附近时，黄色的MIL算法和红色的L1APG开始有脱离目标中心位置的趋势，最终在第160帧图像中只有L1APG完全丢失目标。在图4-15的第68帧中，当目标移动到电桩的后面时，有几类算法偏离了目标中心位置，当目标离开电桩后面时，除了绿色的本文算法还能捕获到目标，红色的L1APG和MEEM都捕获到其他目标上去了，而剩下的都完全偏离目标。

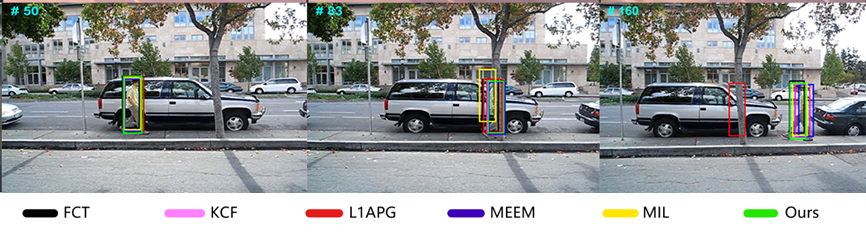
图4-14 本算法与其他5种算法在David3视频序列上的跟踪结果对比

图4-15 本算法与其他5种算法在Jogging1视频序列上的跟踪结果对比

综合来看，虽然本文的算法还不能完全超越其他算法，在视频序列测试中也体现出该算法和其他算法之间的明显差距。但是，相较于原来的DSST算法，PSR判据的作用是显而易见的，通过以峰值旁瓣比作为参照，该算法能够在恰当的时间更新目标模板，持续捕获目标中心位置，在大多数情况下能够担当图像跟踪的重要任务。

本章小结

本章内容主要介绍了我们的具体的实验环境和参数变量，例如进行实验时所用的硬件和软件平台，以及做对比试验时所设置的参照。然后还介绍了对比实验的具体流程和方法，我们以TColor-128数据集为测试基础，在此之上我们进行了消融实验，在控制变量的条件下，本文算法在精确度和成功率上都表现出符合预期的显著效果。最后我们对包括本文算法在内的六种跟踪器进行总体性能评估，从综合效果来看，改进后的DSST算法的跟踪性能处于中上水平，在大部分干扰因素下都表现出不错的鲁棒性，说明具有较高的实用性。

---

第五章 总结与展望

项目的经济及相关安全与环境影响分析

本文设计只针对基于DSST目标跟踪的相关软件仿真部分，不涉及实物上机部分。在设计准备前期时，我依据指导老师的建议详细阅读了与DSST算法相关的参考文献，例如：《Discriminative Scale Space Tracking》、《Real-time long-term tracking with reliability assessment and object recovery》以及《An improved correlation filter tracking method with occlusion and drift handling》等，这些文献让我对目标跟踪领域有了全新的认识。本设计开发成本低，在合理借助网上的相关实验素材以及老师的指导下，耗时两个月实现了一个可以有效自适应更新目标模板的改进DSST算法。本项目在目标跟踪和计算机视觉应用领域十分广泛，特别是对于视频图像捕捉有很大的帮助和参考价值。

总结

目前，目标跟踪在世界各国军事上的海岸视监系统、空中管制系统、以及定位和防卫系统中获得了非常广泛的使用。该技术还在民用的智能驾驶系统、视频监控以及安防系统等得到更多的应用。信息和传感器技术的换代是必然的，近几年，用于单方面的传感器和目标跟踪技术得到了多种程度的完善与发展。不过，总依赖单模传感器来达到目标跟踪的任务，是很难满足在现实生活中更高的需求和应用，所以，为了提高跟踪性能，我们需要将计算机视觉的技术用在目标跟踪系统中去。

在本文中，我们介绍了在图像跟踪领域中相关滤波的作用和原理，为后文的DSST算法打下基础。然后提到了常用的公共数据集，这是对目标跟踪算法的检测，比如OTB100和TColor-128在这一方面就具有权威性和可靠性。在讨论模板自适应更新时，我们发现了DSST算法在尺度变换和目标遮挡等干扰因素下的不足之处，同时也发现通过峰值旁瓣比可以判断出当前目标是否被遮挡，于是结合这一点我们改进了DDST算法。最后以TColor-128数据集中的七组视频序列来作为测试代表，在最后的表现效果中，改进后的DSST算法已经明显好于原算法，并在大部分测试条件下不输于其他算法。

展望未来

虽然本文算法在目标跟踪方面已经有了不错表现，但是对于少数情况还是有急需改进的地方，这样更有助于投入到实际使用中去。除了可以使用PSR峰值旁瓣比来更新目标模板，我们还可以用颜色信息来作为一个判断依据。不仅如此，在实际情况中，我们还需要考虑算法的效率问题，要做到又快又好，这才是好算法。同时，在实验中还有一个容易忽略的问题就是相似目标遮挡，比如在公路上，相似的汽车或行人与跟踪目标相遇到一起，这样就可能导致跟踪发生漂移，这是就需要更强有力的特征依据来辨别目标。

---

致谢

一个人的一生能遇到几位可以给自己的成长带来改变的老师，是十分幸运的事。一篇完整的论文从立意到完笔也都离不开老师的悉心指导，而本论文的工作就是在我的导师刘老师帮助下完成的。在此过程中，我遇到了很多毫无思路的问题，甚至偶尔也会有走投无路的想法在干扰我的思维，但是这都被平易近人的刘骏老师热情地解决了，我很感谢老师对我的支持与帮助，这给我四年大学生活的结尾留下了难忘的回忆，同时这也离不开学校对我的栽培，让我拥有了一个难得的学习成长的舒适环境。

当然，本人能一步一步走到今天，背后更离不开父母、同学等亲朋好友的支持与鼓励。人是社会性动物，脱离了群体是没法单独生活的，所以我们学会了合作与互助，就像“人”这个字的结构一样，我们如同这一撇一捺，相互支撑相互依靠。在未来的生活，我会克服重重困难，一路前进。

最后，感谢百忙中参与论文审核和答辩工作的专家和老师。

---

参考文献

¹. 孟琭, 杨旭. 目标跟踪算法综述[J]. 自动化学报, 2019, 045(007):1244-1260. ↩

². Lu H C, Fang G L, Wang C, et al. A novel method for gaze tracking by local pattern model and support vector regressor[J]. Signal Processing, 2010, 90(4):1290-1299. ↩

³. Ben Mabrouk A, Zagrouba E. Abnormal behavior recognition for intelligent video surveillance systems: A review[J]. Expert Systems with Applications, 2018, 91(jan.):480-491. ↩

⁴. Kastrinaki V, Zervakis M, Kalaitzakis K . A survey of video processing techniques for traffic applications[J]. Image & Vision Computing, 2003, 21(4):359-381. ↩

⁵. Kastrinaki V, Zervakis M, Kalaitzakis K . A survey of video processing techniques for traffic applications[J]. Image & Vision Computing, 2003, 21(4):359-381. ↩

⁶. 赵俊青. 智能视频分析中目标跟踪算法的改进与实现[D]. 电子科技大学. ↩

⁷. Avidan, S.: Support vector tracking. IEEE Trans. Pattern Anal. Mach.Intell. 26(8), 1064–1072 (2004). ↩

⁸. Saffari, A., et al.: On-line random forests. International Conference onComputer Vision, Kyoto, Japan, 1393–1400 (2009). ↩

⁹. Babenko, B., et al.: Robust object tracking with online multiple instancelearning. IEEE Trans. Pattern Anal. Mach. Intell. 33(8), 1619–1632 (2011). ↩

¹⁰. Kalal, Z., et al.: Tracking-Learning-Detection. IEEE Trans. Pattern Anal.Mach. Intell. 34(7), 1409–1422 (2012). ↩

¹¹. Zhong, W., et al.: Robust object tracking via sparsity-based collaborative model. Computer Vision and Pattern Recognition, Rhode Island, USA 1838–1845 (2012). ↩

¹². Chen, D., et al.: Description-discrimination collaborative tracking. European Conference on Computer Vision, Zurich, Switzerland, 345–360 (2014). ↩

¹³. Zhang, J., et al.: MEEM: Robust Tracking via Multiple Experts UsingEntropy Minimization.European Conference on Computer Vision,Zurich, Switzerland 188–203 (2014). ↩

¹⁴. Wu, Y., et al.: Online object tracking: a benchmark. Computer Vision and Pattern Recognition, Portland, OR, USA, 2411–2418 (2013). ↩

¹⁵. Bolme D S, Beveridge J R , Draper B A , et al. Visual object tracking using adaptive correlation filters[C]// The Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2010, San Francisco, CA, USA, 13-18 June 2010. IEEE, 2010. ↩

¹⁶. Henriques, J.F., et al.: Exploiting the circulant structure of tracking-bydetection with kernels. European Conference on Computer Vision, Florence, Italy 702–715 (2012). ↩

¹⁷. Huang, Z., et al.: Learning Aberrance Repressed Correlation Filters forReal-Time UAV Tracking. International Conference on Computer Vision,Seoul, Korea, South 2891–2900 (2019). ↩

¹⁸. Valmadre, J., et al.: End-to-end representation learning for correlation filterbased tracking. Computer Vision and Pattern Recognition, Honolulu, HI,USA 5000–5008 (2017). ↩

¹⁹. Bertinetto, L., et al.: Fully-convolutional siamese networks for object tracking. European Conference on Computer Vision, Amsterdam, The Netherlands, 850–865 (2016). ↩

²⁰. Ma, C., et al.: Hierarchical convolutional features for visual tracking. International Conference on Computer Vision, Santiago 3074–3082 (2015). ↩

²¹. Danelljan, M., et al.: Beyond Correlation Filters: Learning ContinuousConvolution Operators for Visual Tracking. European Conference onComputer Vision, Amsterdam, The Netherlands 472–488 (2016). ↩

²². Danelljan, M., et al. ECO: Efficient Convolution Operators for Tracking. Computer Vision and Pattern Recognition, Honolulu, HI, USA 6931–6939 (2017). ↩

²³. Kalal, Z., et al.: Tracking-Learning-Detection. IEEE Trans. Pattern Anal. Mach. Intell. 34(7), 1409–1422 (2012). ↩

²⁴. Ma, C., et al.: Long-term correlation tracking. Computer Vision and Pattern Recognition, Boston, MA, USA, 5388–5396 (2015). ↩

²⁵. Hong, Z., et al.: Multi-store tracker (muster): A cognitive psychologyinspired approach to object tracking. Computer Vision and Pattern Recognition, Boston, MA, USA, 749–758. ↩

²⁶. Dai, W., et al.: Long-term adaptive tracking via complementary trackers.IET Image Processing 13(9), 1569–1577 (2019). ↩

²⁷. Lukezic, A., et al.: FuCoLoT - A Fully-Correlational Long-Term Trackerr. Asian Conference on Computer Vision, Perth, Australia 595–611(2018). ↩

²⁸. Sun, C., et al.: Correlation Tracking via Joint Discrimination and ReliabilityLearning. Conference on Computer Vision and Pattern Recognition, SaltLake City, UT 489–497 (2018). ↩

²⁹. Bolme, D.S., Beveridge, J.R., Draper, B.A., Lui, Y.M.: Visual object tracking using adaptive correlation filters. In: Proceedings of the IEEE Computer Vision and Pattern Recognition, pp. 25442550 (2010). ↩

³⁰. Dai, K., et al.: Visual Tracking via Adaptive Spatially-Regularized Correlation Filters. Computer Vision and Pattern Recognition, Long Beach, CA4670–4679 (2019). ↩

³¹. Bhat, G., et al.: Unveiling the Power of Deep Tracking. European Conference on Computer Vision, Munich, Germany 493–509 (2018). ↩

³². Yang, F., et al.: Robust visual tracking based on global-and-local search withconfidence reliability estimation. Neurocomputing. 357, 273–286 (2019). ↩

³³. Bolme D S, Beveridge J R , Draper B A , et al. Visual object tracking using adaptive correlationfilters[C]// The Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2010, San Francisco, CA, USA, 13-18 June 2010. IEEE, 2010. ↩